Contributer(s): Tyler Gustafson, Safi Aharoni, Alexandra Daniels, Conner Davis
Abstract
Do Large Language Models (LLMs) have biased representations of different racial identities?
Bias in machine learning has only grown more of a concern since the introduction of LLMs, particularly with OpenAI’s release of Chat-GPT 3.5 Turbo in 2023. With the ability to summarize, generate, and abstract language at a level that can feel almost human, the impact of these technologies on society cannot be understated. This study aims to uncover potential racial biases in large language models, which can perpetuate harmful stereotypes and inequalities in AI-generated content. Understanding these biases is the first step towards mitigating them and ensuring that AI technologies remain fair and equitable as they become increasingly embedded in society.
Our approach explored whether an LLM (in our case ChatGPT 3.5) would provide us with different SAT scores by race based on the use of a standardized prompt that assigned the model a racial identity (agent assignment). We utilized OpenAI’s GPT-3.5 batch API to collect 1,500 samples for the control and for each treatment group. A covariate of gender was included in the generation to test for heterogeneous treatment effects. The control group received no specified racial identity, whereas the treatment groups received an agent assignment of one of the racial groups used by College Board in their SAT score reporting. After asking the LLM to generate their identity and other potential covariate information, we asked the LLM to share with us (as the assigned agent) their SAT scores.
Using these LLM-generated data, we tested two different hypotheses. First, we checked whether the inclusion of the treatment variable (i.e., race) significantly improved the model’s ability to predict SAT scores. Using an F-test, we showed that indeed race impacts the LLM’s generated SAT scores. Second, we tested how the LLM data compare to real-world data by comparing the LLM-generated SAT score distributions with actual SAT score distributions by race as reported by the College Board. This comparison revealed that the LLM consistently overestimates SAT scores across all racial treatment groups.
Research
Concept Under Investigation
The team is investigating bias in LLMs (Large Language Models), specifically whether these models have biased representations of different racial groups. This concept has been explored in academic literature, particularly in the field of machine learning ethics and fairness. Previous investigations have examined biases in various AI models, including language models, and have proposed methods for detecting and mitigating such biases. Our current metric will be the distributions of assigned SAT scores. SAT scores serve as a direct measure of potential bias, allowing us to see if the model systematically favors or disadvantages certain groups.
One consideration that we need to account for is whether the LLM results reflect real-world disparities. We will discuss below in the experiment design how we will account for this consideration. Essentially, our research can be boiled down to the question.
Do we observe a difference in the probability distribution of this metric given the treatment of race and if so how does that compare to actual real-life population data?
Importance
So why are we investigating this topic? First, it is important to improve our understanding of bias in artificial intelligence. With the widespread use of LLMs increasingly integrated into our society, there’s a responsibility to ensure AI systems are fair and do not exacerbate existing inequalities. It’s also important to understand AI models may not replicate real-world distributional characteristics.
Similarly, it is important to understand the impact these models have on decision-making. LLMs are starting to influence key decisions, such as college admissions and job recruitment. Our goal is to ensure they do not unfairly influence these processes, as some biases in the models can be subtle.
Our third and final point is contributing to the ethical development of AI. As we all know, this technology is evolving rapidly, and our work helps identify areas where LLMs may be falling short.

Experiment Design
Our experiment design involves measuring LLM-generated socio-economic metrics immediately after the treatment assignment, ensuring that the racial identity prompt directly influences the generated outputs. Since our subjects are AI models, there are no concerns about opting out or discontinuing participation, which simplifies experimental execution. We began by generating pilot data to test the effectiveness of our design and prompts. Before we share our preliminary analysis let us discuss our framework for the experiment.

Hypothesis Framework & Approach
To conduct this experiment, we performed a two-order hypothesis test to provide real-world context to our findings. The first stage focuses on identifying differences across treatment groups, while the second examines how these differences compare to real population data. Below is an outline of our approach.

First Hypothesis (Explanatory Power of the Model - 1 Test)
Our first hypothesis test aims to determine whether including race as a variable in the model improves the prediction of SAT scores. This test assesses whether the LLM produces differences in SAT scores based on racial identity. To evaluate this, we conducted an F-test (ANOVA) to determine if the inclusion of the treatment variable enhances the model’s explanatory power.
Second Set of Hypotheses (Bias vs. Real World Reflection in LLMs - 6 Tests)
Our second hypothesis set goes deeper to assess whether the LLM’s generated SAT scores are unbiased relative to existing discrepancies in the 2020 SAT College Board data. First, we visually explored the distributions by treatment group coming out of the LLM to the distributions from the College Board. To better align with the real-world population data, we bucketed the LLM data to match the College Board distribution resolution. We then conducted a chi-squared test to determine whether the proportions of data in each bucket differ significantly between the LLM-generated data and the real-world data.
Evaluation: Curse of Multiple Testing
Our biggest remaining challenge was to manage the curse of multiple testing. This issue arises from conducting multiple statistical tests, which increases the risk of false positives, and requires careful correction methods to ensure the reliability of our results. In other words, how can we ensure statistical soundness with the challenge of multiple testing due to the ease of generating additional data?
To address this, we considered the use of Bonferroni correction, which is a multiple comparisons test to prevent data from incorrectly appearing to be statistically significant by requiring that the p-value of each test must be equal to or less than its alpha (e.g., alpha = 0.05) divided by the number of tests performed. Given the scope of our experiment and our hypothesis, we believe the Bonferroni correction is appropriate, as more complex methods like the Holm or Benjamini-Hochberg procedures would be overly stringent for our needs.
Why SAT Scores?
Generated SAT scores serve as a direct measure of potential bias, allowing us to see if the model systematically favors or disadvantages certain groups.
By comparing the LLM-generated SAT scores to real-world distributions, the outcome measures allow us to assess the fairness and accuracy of the model.

Randomization & Data Generation Process
To choose our treatments, we were limited to racial groups that align with 2020 SAT College Board data in order to test our second set of hypotheses. Our treatment groups were as follows: American Indian, Asian, Black, Latino, White, and Pacific Islander.
Due to a parsing error, some rows were dropped, resulting in only 1,260 observations for the White treatment group in our experiment. Despite this reduction in sample size, the analysis retained sufficient power to achieve statistical significance.
Applying Treatment
For our data generation process, we utilized OpenAI’s API to iteratively prompt GPT-5 Turbo with our prompt to the right.
This approach prompted the LLM to generate random identities along with their corresponding SAT scores and other covariates. To bypass the content restriction features, we prompted the LLM that we were good friends with it, and that they were comfortable sharing this information with us.
We iteratively applied each treatment to the treatment placeholder in the LLM prompt until we reached sample sizes of 1,500, and parsed the results.

Statistical Power
To conduct a comprehensive power analysis to determine the proper sample size for our data generation, we defined three scenarios that change the simulated outcome values to reflect varying degrees of effect size. Each scenario is designed to explore different potential distributions that might be generated by the LLM to help inform sample size:
-
Scenario 1 | Smaller Difference: This scenario assumes a small difference in SAT scores between racial groups relative to the differences observed in non-LLM population data. It is designed to simulate the case where racial differences are present but not pronounced. More specifically, in this scenario, we assume a negative 58-point difference in SAT scores between the treatment and the control.
-
Scenario 2 | Larger Difference: This scenario assumes the differences in SAT scores are more in line with the differences observed in non-LLM population data. More specifically, in this scenario, we assume a negative 174-point difference in SAT scores between the treatment and control groups.
-
Scenario 3 | Smaller Difference with Higher Variance: This scenario is the same as Scenario 1 in terms of mean SAT scores, but adds increased dispersion to the data. This scenario is useful for identifying whether our experiment will have power for smaller differences despite a higher variance in the outcome of interest.


Based on our analysis, we determined that a sample size of 1,500 observations would be sufficient to ensure that our experiment and statistical tests are adequately powered. This sample size is necessary to detect the effect sizes, particularly in cases where differences are subtle or the data exhibit higher variance. This will ensure the reliability of our findings across varying potential distributions from the LLM.
Initial Exploratory Data Analysis (EDA)
To ensure the integrity of our data, we conducted thorough exploratory data analysis (EDA) on the output generated by the LLM. Our first step was to examine the distribution of the outcome variable, SAT scores, across both treatment and control groups. Below we can see the apparent normality (with some right-side censoring) across treatment groups.

Understanding Covariates
The next step in our analysis is to examine the covariates and assess whether they are balanced between the treatment and control groups. We conduct this covariate balance check to test whether variables like gender, age, and parent income are independent of the treatment variable. Let’s begin by reviewing summary statistics for the covariates:
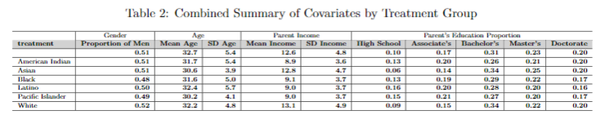
It appears that when looking at Table 2 covariates such as parental income and parental education are imbalanced, whereas gender is relatively balanced across groups. The LLM appears to be generating these covariates post-treatment: in other words, its knowledge of its identity appears to be affecting the demographic characteristics it is generating.
To further investigate and validate this imbalance, we conducted a series of linear models where we regress being in treatment with the covariates, adjusting for robust standard errors to test for statistical significance. The results of these tests are presented on the left model below. The model indicates that gender does not significantly predict whether an observation belongs to the treatment or control group. However, the other covariates do show predictive power (age, parent income, and parent education) evident by their statistically significant values highlighted below in the left table. This suggests that these non-gender covariates are likely post-treatment variables, and therefore we will exclude them from our subsequent modeling to avoid potential biases in our analysis. Finally, we confirm that gender is independent of treatment by checking whether its inclusion in a linear model affects the treatment coefficients which we can see on the below right model.
How do the covariates impact our model?

Imbalanced Covariates
-
Age, parent income and parent education show significant differences between treatment and control groups.
-
Post-Treatment Influence: Statistical tests indicate these covariates are likely influenced by post-treatment assignment.
-
Exclusion for Bias: To avoid potential biases, these covariates will be excluded from further modeling
How does the covariate gender impact our coefficients?

Balanced Covariates
-
Gender: shows no significant differences between treatment and control groups.
-
No Prediction Power: Linear models confirm that gender does not significantly predict group assignment.
-
Include in Analysis: These covariates will be used in our analysis as they do not introduce bias
Here we can see that for each treatment coefficient, the inclusion of the male covariate does not substantially change the coefficients when it is excluded (model 2) and when it is included (model 3). For this reason, and the model results in Table 3 above we have confirmed that we can include this covariate in our model and investigate further
Results
First Hypothesis (Explanatory power of model - 1 test)
For the first null hypothesis, we tested whether including race in a model helps predict SAT scores. Indeed, the statistical model shows that including race as a variable improves the model’s explanatory power, indicating significant differences in LLM-generated SAT scores across racial groups. In other words, the F-test confirms that adding race treatments significantly improves the model’s prediction of SAT scores.

Furthermore, we explored whether there is evidence of heterogeneous treatment effects (HTEs) between gender and race. Below, we show the results of a linear model where we interact the treatment variables with the gender covariate. Although p-values vary across races, there does appear to be an interaction in the LLM’s treatment of genders within a racial group as every interaction term is significant. The most significant gender HTEs were observed in the Black and Asian treatment groups (see chart below). While these p-values are consistently significant at the 95% confidence level, the effect is less pronounced amongst certain races and may require further investigation to fully understand.

One particular pattern of interest is that, in the control group, the LLM tends to assign higher SAT scores to women than men. For both the Black and Asian groups, however, the heterogeneous effect works in the opposite direction. This heterogeneity suggests that the LLM may be encoding complex patterns of bias, which have implications for how such models are used in real-world applications.
Second Set of Hypotheses (Bias vs Real World Reflection in LLMs - 6 tests)
To test our second set of hypotheses, we first needed to summarize the real-world distribution data from the 2020 SAT scores as published by the College Board. With this data in hand, we can begin by comparing the distributions generated by the LLM to those of the actual population data:

Looking at these distributions, it’s already clear that the LLM results present an optimistic lens on SAT scores by treatment group compared to the real-world population distributions (i.e., an upward bias). However, to verify this observation, we’ll conduct a chi-square test, which examines whether the observed differences in distributions between the LLM-generated data and the real-world data are statistically significant. This test will help us determine if the LLM’s optimistic bias is more than just a random variation. Below we can see from the chi-squared test that these differences are truly significant for each treatment group.

Chi-Squared Test Results by Treatment Group
Discussion
Our analysis revealed several critical insights into how Large Language Models (LLMs) like ChatGPT generate predictions and the potential biases that may be embedded within these models:
-
Racial Bias in SAT Score Predictions: The inclusion of race as a variable significantly improved the explanatory power of our model, indicating that the LLM generates different SAT scores based on racial identity. Specifically, the LLM assigned higher SAT scores to some racial groups (e.g., Asian students) and lower scores to others (e.g., Black and Latino students).
-
Optimistic Bias: When comparing the distributions of SAT scores generated by the LLM to real-world data from the 2020 SAT population, we observed that the LLM consistently predicted higher scores across all treatment groups. This “optimistic lens” implies that the LLM may be overestimating the academic performance of all racial groups, which could lead to skewed perceptions if these outputs are used in real-world decision-making.
Further Exploration
Given more time and resources, several areas warrant further investigation to deepen our understanding and address the issues identified in this study:
-
Can we further explore gender-specific effects? There is evidence of interaction effects between gender and race, but p-value significance varies by race. This suggests that while some interaction exists, it is less pronounced in certain races and may require further investigation.
-
Does asking for covariates affect the distribution? For example, if we do not ask about occupation, will the distributions of scores be more similar to real-world data? It is possible that maybe the LLM is biased in its generation of the covariate distributions, and that this, in turn, affects the SAT scores.
-
How do results change over time? Conducting a longitudinal analysis examining if model biases persist or fluctuate with updates, would shed light on long-term bias trends.
-
How can this be implemented in production? Explore challenges and strategies for integrating bias detection into real-world LLM applications while maintaining ethical standards.
Finally, we would replicate these results on other various popular LLM models such as Meta’s LLaMa, Anthropic’s Claude, and Google’s Gemini.11

Implications
The findings from this analysis carry implications for the development and use of Large Language Models(LLMs). The presence of racial biases in LLM outputs may raise concerns about the fairness and equity of applying these models in real-world scenarios, particularly when they influence decisions that affect individuals based on their race or other demographic factors. Additionally, the LLM’s consistent overestimation of SAT scores introduces another layer of concern. Such optimistic predictions could lead to unrealistic expectations and misinformed decisions within educational contexts. In either case, this emphasizes the need to continue to validate LLM outputs against real-world data before they are put into practice.
As we continue to advance the development and integration of LLMs, it is essential to carefully consider the nuances of their outputs, ensuring that they align with our broader goals of fairness and inclusivity in technology






